Damit das mikroskopische Simulationssystem die makroskopischen experimentellen Ph?nomene widerspiegelt, ist es notwendig, das simulierte Objektsystem durch periodische Randbedingungen periodisch zu replizieren, um Randeffekte zu vermeiden, die in der Praxis nicht vorhanden sind. Grunds?tzlich erfordert die theoretische Untersuchung jedes molekularen Systems die L?sung der zeitabh?ngigen Schr?dinger-Gleichung. In der Praxis wird jedoch mehr auf die Flugbahn des Kerns geachtet. Eine solche Trajektorie kann durch L?sen der klassischen mechanischen Bewegungsgleichung unter Verwendung der Born-Oppenheimer-N?herung erhalten werden. Alder und Wainwright haben gesagt, dass Computersimulationsexperimente zu einer wichtigen Brücke werden, die makroskopische experimentelle Ph?nomene und mikroskopische Natur verbindet. Nach 10 Jahren ihrer ersten Molekulardynamik-Simulationsexperimente schlug der franz?sische Physiker Verlet einen Integrationsalgorithmus für Newtons Bewegungsgleichungen vor. Gleichzeitig wird ein weiterer Satz von Algorithmen zur Generierung und Aufzeichnung von Paaren benachbarter Atome vorgeschlagen, der die Berechnung der Wechselwirkung zwischen Atomen stark vereinfacht. Diese beiden Algorithmen sind in einigen Varianten in der Praxis noch weit verbreitet [1, 2].

In den letzten Jahrzehnten wurde eine Vielzahl von Simulationsmethoden auf atomarer Ebene entwickelt, darunter Gitterstatik, Gitterdynamik, Monte Carlo und Molekulardynamik. Unter ihnen ist die Molekulardynamik besonders geeignet für die Untersuchung der plastischen Verformung. Es untersucht das Echtzeitverhalten des Verformungsprozesses durch die L?sung der Newtonschen Gleichung des atomaren Wechselwirkungssystems einiger definierter interatomarer Wechselwirkungspotentialfunktionen und schlie?t die Nichtvereinfachung des Gitters ein. Harmonizit?t, H?henungleichm??igkeit der Eigenspannung und Einschwingverhalten des Systems.

Die Molekulardynamik beruht haupts?chlich auf der Newtonschen Mechanik, um die Bewegung des molekularen Systems zu simulieren und Proben aus Systemen zu extrahieren, die aus verschiedenen Zust?nden des molekularen Systems bestehen, wodurch das Konfigurationsintegral des Systems berechnet und das System basierend auf den Ergebnissen der Konfiguration weiter berechnet wird Integral. Thermodynamische Gr??en und andere makroskopische Eigenschaften. Es l?st die Bewegungsgleichung für ein Mehrk?rpersystem aus Kernen und Elektronen. Es ist eine Berechnungsmethode, die das Systemdynamikproblem einer gro?en Anzahl von Atomzusammensetzungen l?sen kann. Es kann nicht nur die makroskopischen Entwicklungseigenschaften einer Substanz direkt simulieren, sondern auch mit den Testergebnissen übereinstimmen. ?hnliche Berechnungen k?nnen auch ein klares Bild der Mikrostruktur, der Partikelbewegung und ihrer Beziehung zu makroskopischen Eigenschaften liefern und bieten eine leistungsstarke technische Unterstützung für die Entwicklung neuer Theorien und Konzepte.

Das Objekt der Molekulardynamik ist ein Partikelsystem. Die Wechselwirkung zwischen Atomen im System wird durch die Potentialfunktion beschrieben. Daher spielt die richtige Auswahl des Typs der potenziellen Funktion und ihrer Parameter eine wichtige Rolle für die Simulationsergebnisse. In den meisten F?llen vereinfacht die potentielle Energiefunktion die Beschreibung der geometrischen Verformung des Moleküls insofern, als nur der einfache harmonische Term und die trigonometrische Funktion verwendet werden; Anstelle der Wechselwirkung zwischen den Bindungsatomen werden nur die Coulomb-Wechselwirkung und das Lennard-Jones-Potential verwendet. Kombiniert, um zu beschreiben. Unter diesen ist die Beschreibung der Wechselwirkungskraft zwischen Atomen normalerweise empirisch oder semi-empirisch, was die Recheneffizienz verbessern kann, aber die Mehrk?rpereigenschaften der Elektronenbindung, insbesondere die Komplexit?t in Bezug auf ihre Struktur und Chemie in, nicht vollst?ndig aufdecken kann die N?he von M?ngeln. Selbstkonsistente Variationsfunktion. Die EAM-Potentialfunktion (Embedded-Atom-Modell) von Daw und Baskws kombiniert die Mehrk?rpereigenschaften der elektronischen Bindung in gewissem Ma?e.

Die Zuverl?ssigkeit der Potentialfunktion h?ngt haupts?chlich von der Genauigkeit der Kraftfeldparameter ab, und die Kraftfeldparameter k?nnen durch Anpassen experimenteller Beobachtungsdaten und quantenmechanischer Ab-initio-Daten erhalten werden. Derzeit ist das am weitesten verbreitete molekulare Kraftfeld bei der Simulation biologischer makromolekularer Systeme das CHARMM-Kraftfeld und das AMBER-Kraftfeld, das das molekulare Kraftfeld für die frühe Untersuchung biologischer Makromoleküle ist. Bestehende Kraftfeldparameter werden immer noch kontinuierlich optimiert und die Arten der abgedeckten Moleküle nehmen ebenfalls zu. Das grobk?rnige Modell gewinnt in der rechnergestützten biophysikalischen Forschung zunehmend an Bedeutung, da in diesem Modell grobk?rnige Partikel definiert sind, die mehreren Atomen oder Atomgruppen oder sogar Molekülen im Allatommodell entsprechen. Die Anzahl der Partikel im System wird reduziert, so dass die Zeit- und Raumskala der Simulation erheblich verbessert werden kann, aber auch die atomaren Details verloren gehen. Auf diesem Modell basierende molekulardynamische Simulationen eignen sich zur Untersuchung langsamer biologischer Ph?nomene oder biologischer Ph?nomene, die von gro?en Baugruppen abh?ngen.

Das Grundprinzip beim Entwerfen eines grundlegenden Kraftfelds besteht darin, den Rechenaufwand in einem Zeitschritt zu minimieren, um den Simulationsma?stab zu maximieren. Dies ist besonders wichtig für das gesamte Atomkraftfeld, auch für das sogenannte grobk?rnige Modell. Dieses Prinzip ist insbesondere dann sehr wichtig, wenn Sie Zeitskalen von Mikrosekunden oder sogar Millisekunden simulieren m?chten.

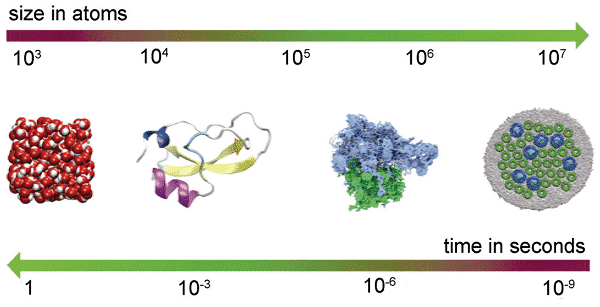
1 zeigt die umgekehrte Beziehung zwischen den zeitlichen und r?umlichen Dimensionen der Molekulardynamik von links nach rechts in der Figur: (1) Wasser, die Grundkomponenten der Zellen; (2) Rinder-Trypsin-Inhibitor, ein Enzym, dessen "Atmungsverhalten im Millisekunden-Zeitma?stab untersucht werden kann; (3) Ribosomen, ein komplexes biologisches Ger?t, das genetische Informationen entschlüsseln und Proteine produzieren kann; (4) lila bakterielle photosynthetische Membranfragmente; Mit 25 Millionen Atomen zeigt die Abbildung den Lichtsammelkomplex, der in die Phospholipid-Doppelschicht und das photochemische Reaktionszentrum eingebettet ist.

Abbildung 1 Skalenbeziehung zwischen Zeit und Raum der klassischen Molekulardynamik

Mit dem schnellen Wachstum von Computerprozessoren und der Entwicklung von massiv parallelen Computerarchitekturen, der Kombination von massiv parallelisierten oder propriet?ren Architekturtechniken mit skalierbaren molekulardynamischen Programmen reichen Computersimulationen von Versetzungen bis zu korngrenzenbasierten Verformungsmechanismen. Das gesamte Spektrum der Korngr??en er?ffnet neue M?glichkeiten zur Erforschung der Forschungsgrenzen von Materialsystemen.

Zum Beispiel haben William Gon?alves et al. verwendeten die Wolf BKS (van Beest, Kramer und van Santen) -Potentialfunktion, um die Wechselwirkung zwischen Atomen unter Verwendung des gro?r?umigen Atom / Molekular-Parallel-Simulators LAMMPS (Large-Scale Atomic / Molecular Massively Parallel) zu beschreiben. Simulator) untersuchte die Molekulardynamik der Elastizit?t und Festigkeit von Silica-Aerogelen. Sie verwendeten den Velocity-Verlet-Algorithmus und den Zeitschritt von 1,0 fs und verwendeten periodische Randbedingungen in alle drei Richtungen.

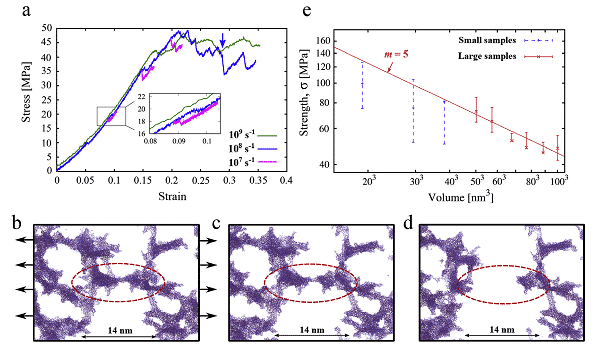
2 ist ein schematisches 3D-Diagramm einer simulierten gro?volumigen Probe mit mehr als 7.000.000 Atomen und einem 20 nm dicken Probenabschnitt und einer teilweise vergr??erten Ansicht (blau ist ein Sauerstoffatom, rot ist ein Siliziumatom) und 3 (a ) ist ein 803 nm 3 Aerogel. Die Probe wurde einem einachsigen Zugtest unterzogen, um eine Spannungs-Dehnungs-Kurve von 300 K zu erhalten, (bd) ist ein typisches duktiles Bruchbild und (e) eine logarithmische Beziehung zwischen Zugfestigkeit und Probenvolumen. Sie analysierten, dass die Gr??e der simulierten Probe mindestens das 8-fache der Porengr??e betr?gt, um eine ordnungsgem??e Bewertung mechanischer Eigenschaften wie der Elastizit?t sicherzustellen, w?hrend das Silica-Aerogel mit einer positiven Oberfl?chenh?he eine relativ geringe Dehnungsrate erfordert, um quasi zu gew?hrleisten. statische Bedingungen.

Abbildung 2 Simulierte Silica-Aerogelprobe (mehr als sieben Millionen Atome)

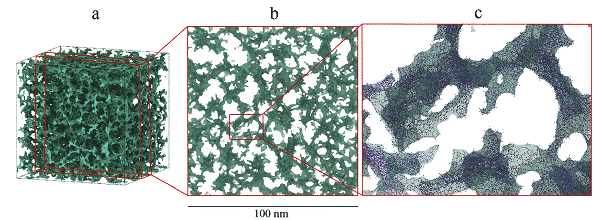
Fig. 3 Spannungs-Dehnungs-Kurve (a), Festigkeits-Volumen-Beziehung (e) und Bruchbild (bd) des einachsigen Zugversuchs

Im Allgemeinen betr?gt die kritische Korngr??e dc etwa 20 bis 30 nm, und die gr??ere Verformung für die Korngr??e (50 bis 100 nm) wird haupts?chlich durch Versetzungen bestimmt; Wenn die Korngr??e weniger als 30 nm betr?gt, wird sie haupts?chlich vom GB-Verformungsprozess dominiert, und die Korngr??e wird verringert. Dies führt zu einer Abnahme der Festigkeit und der Flie?spannung, dh zu einem "Anti-Hall-Petch-Effekt". Der umfassende Vergleich zwischen Mehrk?rper- und Paarpotentialen, die zur Modellierung von GBs in fcc- und bcc-Metallen verwendet werden, zeigt jedoch, dass es nur geringe qualitative Unterschiede im Verhalten gibt, das durch diese unterschiedlichen Kraftbeschreibungen vorhergesagt wird, was darauf hindeutet, dass Mehrk?rpereffekte das GB-Verhalten m?glicherweise nicht dominieren.

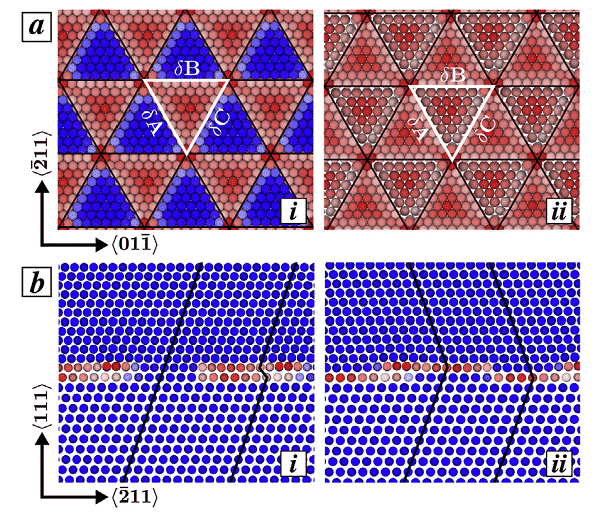
Bejaud, J. Durinck et al. verwendeten eine molekulardynamische Simulation, um die Wechselwirkung zwischen deformierten Zwillingen und nanostrukturierten Cu / Ag-Grenzfl?chen zu untersuchen, analysierten die Auswirkungen der Grenzfl?chenstruktur auf die Keimbildung, Expansion und Verdickung von Zwillingen und erkl?rten die Fehlpaarungsgrenzfl?che. Die Rolle des Versetzungsgitters. Abbildung 4 zeigt das Shockley-Teilversetzungsgitter (hervorgehoben durch schwarze Linien), das Dreiecksmuster (wei?er Abschnitt) und die Stapelfehlerverteilung an der Schnittstelle. Unter diesen ist das Atom gem?? dem zentralen Symmetrieparameter gef?rbt, das blaue Atom befindet sich in der perfekten FCC-Umgebung und das rote Atom befindet sich im Stapelfehler oder im Twinning-Fehler.

4 (a) Draufsicht auf Cu- und Ag-Atome entlang der Grenzfl?che: (ai) COC-Grenzfl?che, (a.ii) TO-Grenzfl?che, (b) Seitenansicht entlang der X = <011> -Richtung: (bi) in COC In der Grenzfl?che und der Fall, der koh?rente Bereich wechselt mit dem inh?renten Stapelfehlerbereich (ISF), (b.ii) der TO-Grenzfl?che, und der doppelte Defektbereich existiert kontinuierlich in der Cu-Schicht und der Ag-Schicht.

5 zeigt die Spannungs-Dehnungs-Kurve und das Atomverh?ltnis von Zwillingen als Funktion der Dehnung. Durch Analyse fanden sie heraus, dass die Grenzfl?che direkt oder indirekt die Keimbildung von Zwillingsversetzungen durch Lomer-Versetzungen induzieren kann und wie die heterogene Grenzfl?chenstruktur die verschiedenen Schritte des mechanischen Zwillingsprozesses beeinflusst, wodurch die Bildung von Tantal im nanostrukturierten Cu / Ag beeinflusst wird. Die Gr??e des Kristalls. Diese atomare Methode bietet einige nützliche theoretische Grundlagen für den mechanischen Twinning-Prozess in nanoskaligen Verbundwerkstoffen.

5 (a) Spannungs-Dehnungs-Kurve, (b) Atomverh?ltnis von Zwillingen als Funktion der Dehnung

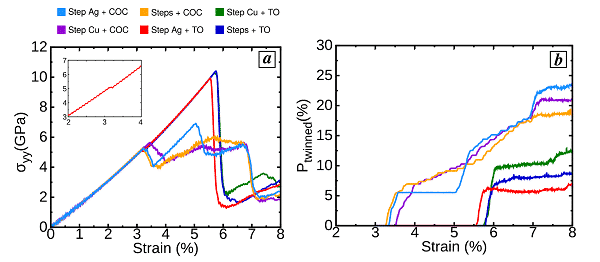
Das Entwerfen von Mehrschichtmaterialien zur Anpassung der mechanischen Eigenschaften ist ein hei?es Thema bei der Steuerung des Verformungsmechanismus, da durch Zwillingsbildung die mechanischen Eigenschaften von Nanoschichten und nanokristallinen Materialien berücksichtigt werden k?nnen. In dieser Hinsicht liefert diese Studie den Schlüssel zum Verst?ndnis des Mechanismus der Interaktion mit zwei Schnittstellen und unterstützt die Ansicht, dass heterophasische Schnittstellen Twinning f?rdern.

Bei ultrafeinen Schichtverbundwerkstoffen, die hcp-Strukturmetalle mit niedriger Symmetrie enthalten, kann eine gro?e Anzahl von Heterogrenzfl?chen effektiv Defekte wie Leerstellen und Zwischengitteratome absorbieren, die durch Kernbestrahlung verursacht werden, und hcp-Metalle selbst haben eine geringe Dichte, spezifische Festigkeit und in den letzten Jahren , haben hexagonale Vielschichtmaterialien aus Ti, Zr, Mg und anderen Metallen aufgrund ihrer hohen spezifischen Steifigkeit und guten elektrischen und thermischen Leitf?higkeit begonnen, die Aufmerksamkeit der Menschen auf sich zu ziehen. Im Vergleich zu fcc- und bcc-Metallen mit hoher Kristallstruktursymmetrie hat hcp-Metall jedoch eine schlechte plastische Verformungsf?higkeit bei Raumtemperatur, was die Verwendung verwandter Verbundmaterialien einschr?nkt.

Zus?tzlich zur r?umlichen und zeitlichen Aufl?sung der atomaren Skala kann die molekulardynamische Simulation das Verhalten des vollst?ndig charakterisierten idealisierten Nanokristallmodells wie Grenzfl?chenstruktur, treibende Kraft und atomaren Mechanismus beschreiben. Andererseits kann es sich um sehr hohe Korngrenzen und -positionen handeln. Das gro?e plastische Verformungsverhalten wurde bei der falschen Dichte beobachtet. Zum Beispiel Versetzungskeimbildungsmechanismus, Korngrenzenl?schung, mechanische Zwillingsbildung in nanokristallinem Al, Verringerung der Korngr??e von Versetzung zu Korngrenzen-basiertem Verformungsmechanismus, Beobachtung des Scherbandes und seiner Bruchfl?chenbeziehung.

Darüber hinaus hat die Dynamik im praktischen Anwendungs- und Forschungsprozess, dem theoretischen Modell für verschiedene Problembeschreibungen und -auswahlen, viele theoretische Zweige entwickelt, auf die sich beispielsweise Jian Han, Spencer L. Thomas von der University of Pennsylvania und andere verlassen die Kraft der Grenze Die Beschreibung der Trennung fasst das Konzept der Korngrenzendynamik polykristalliner Materialien zusammen, Zheng Ma et al. untersuchten die Ausf?llungskinetik von FeCO3 sowie die Oberfl?chen- / Grenzfl?chenkinetik.